Osnovna osnova za vse nauke, ki poznajo svet, je matematiko. Točna znanost uporablja formaliziran jezik ter preučuje vrstni red, strukturo in razmerja na izbranih abstraktnih predmetih. Vsi učenci ne marajo matematike zaradi nje kompleksnost in zmeda, najverjetneje pa zato nerazumevanje. Trajne spremembe v zvezi z matematiko bodo zahtevale predanost, zbranost, doslednost, celo trmoglavost in, kar je najpomembneje, praktične rešitve. V raziskavi je pomembno, da korak za korakom razumemo preprosto in postopoma preidemo na bolj zapleteno, ne da bi pustili ničesar nerazumljivega in slabo zamišljenega.
Obstaja veliko različnih vej matematike, ki so bile dovolj preučene in so se pojavile pred kratkim. V nadaljevanju so opisane osnove matematične analize - osnovni začetni koncepti, definicije in pravila za preučevanje preprostih funkcij ene spremenljivke, izpeljanke in diferenciacije.
Aforizem se je pojavil med osnovnošolci: "Matematika postane res zapletena, ko iz nje izginejo številke." Dejansko se približajo razumevanju nekaterih definicij in zakonov matematične znanosti, tako da se odločijo za pravila s konkretnimi primeri..
Ključne opredelitve
Začnimo s terminologijo - s preprostimi splošnimi pomenskimi pomeni primarnih definicij:
- Spremenljivka - vrednost ali simbol, lahko sprejme katero koli od številnih vrednosti v
določeno območje (teža ali višina otroka)
- Funkcija - namen, delo, dejavnost, specifično delovanje na spremenljivki, označujemo f (x) (odvisnost teže otroka od njegove višine)
- Omejiti - meja, meja, rob (obzorje - vidno polje)
- Izvedeni finančni instrumenti - tvorjen, sekundaren, ki teče iz drugega, označujemo f '(x) (hitrost pri premikanju)
- Diferencialno - razlika, razlikovanje, ločitev.
Funkcija je samo
Funkcija je rezultat tega, kar počne s spremenljivko, kar je rezultat izračuna. To je razmerje elementov, pri katerem sprememba ene spremenljivke povzroči spremembo druge. F (x) razdelite na preproste in zapletene.
Za prikaz odvisnosti se uporabljajo naslednje metode: algebrska, grafična, tabela, logika in celo programska oprema.
Numerične odvisnosti se določajo algebraično s pomočjo simbolov spremenljivk, enakovrednosti in neenakosti (≤ in>), sestavi enačba oblike: y = f (x), tukaj je x spremenljivka ali argument in y ali f (x) je funkcija. Za vsako posebno vrednost spremenljivke x iz dovoljene definicijske domene ustreza določena vrednost y za dano f (x).
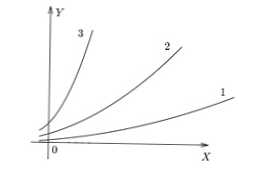
Spodnja slika prikazuje preproste grafe v 3 različnih razmerjih. Vidimo, da v f (x) 3 največjo vrednost y dobimo za x specifično, v f (x) 1 - najmanjšo.
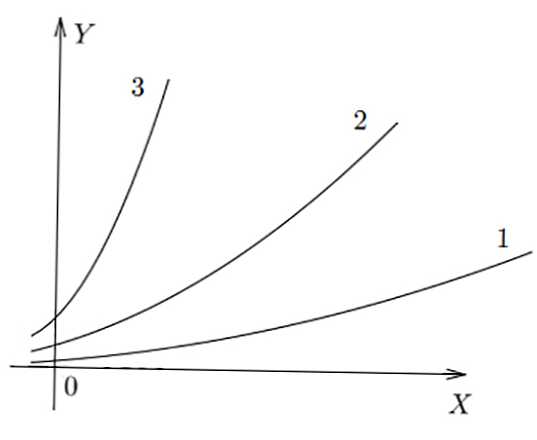
Funkcija
Razlikujemo naslednje elementarne izraze: linearni (neposredni), kvadratni (parabola), kubični, hiperbola, eksponentni, logaritmični, trigonometrični (prikazano v spodnji tabeli).
Za analizo vsakega tipa f (x) so določene njihove inherentne lastnosti (navedene spodaj), za to pa se uporabljajo koncepti izpeljanih in diferencialnih.
Izvedbena funkcija
Izvedeni finančni instrumenti - operater, ki za izvirno f (x) po zakonih diferenciacije pridruži še eno funkcijo, označuje spremembo primarnega f (x) argumenta x v nekem trenutku. Za podrobno razumevanje le-tega bi se morali ukvarjati s kompleksnejšimi definicijami meje odvisnosti in diferenciacije..
Omejiti - ta opredelitev je dinamična. Izraz, ki x nagiba k, se razume na naslednji način: x pridobi vrednosti, ki so blizu n in se razlikujejo po majhni količini.
Diferencialno - majhna sprememba neke velikosti. Prirast se imenuje delta.
Izpeljanka za f (x) v točki je meja delitve delte funkcije s delto spremenljivke v dani točki, če slednja teži na 0.
Značilnost hitrosti spreminjanja odvisnosti v določeni točki, geometrijsko jo lahko prikažemo kot vrednost porjačenja kota nagiba alfa tangenta na funkcijo.
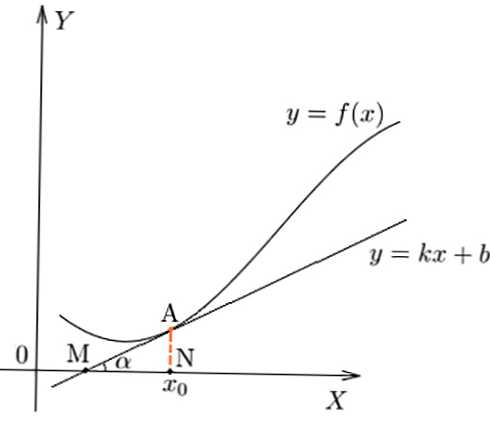
Izvedeni finančni instrumenti
Če je definirana f '(x), se odvisnost imenuje diferencibilna. Iskanje izpeljanke se imenuje diferenciacija. Pravila za izračun f '(x) in ujemanje f' (x) iz osnovne f (x) so podana v spodnji tabeli
Izvedena funkcija tudi deluje
Vsaka odvisnost ima določene lastnosti, s poznavanjem in raziskovanjem pa lahko analizirate naravo stanja in spremembe f (x).
Glavne lastnosti:
- Podatki o definiciji in vrednosti vrzeli.
- Nič (x)
- Funkcija se v nekaterih intervalih poveča ali zmanjša.
- Pokaže funkciji MAX in MIN, ali obstaja pregib.
- Enako ali liho f (x)
- Omejena in neomejena funkcija.
- Ali obstajajo asimptote.
- Frekvenca f (x).

Funkcije in derivati
Pri določanju značilnosti odvisnosti z uporabo izpeljane se uporabljajo medsebojne povezave lastnosti f '(x) z lastnostmi f (x) in obratno. Karakteristike f '(x) zlahka določimo na funkcijskem grafu, in obratno, značilnosti primarnega f (x) razumemo iz grafa f' (x). Pritrdite bistvo vsake lastnosti funkcije, raziščite in vzpostavite verigo odnosov. Za določitev asimptotov v grafih se uporablja koncept mej..
Spodaj so nekatere značilnosti in odvisnosti f '(x) od f (x):
- Ko se f (x) v intervalu povečuje, je f '(x) pozitiven.
- Če se f (x) v intervalu zmanjšuje, je f '(x) negativen.
- V f (x) točke MAX, f '(x) = 0 v njej ni mogoče določiti, tg tangentnega kota pa se spremeni iz + v -.
- V f (x) točke MIN, f '(x) = 0 v njej ni mogoče določiti, tg kota tangenta pa se spremeni iz - v +.
- Pri upogibanju f (x) v E vrednost f '(x) v točki ni spremenila znaka, f' (x) = 0.
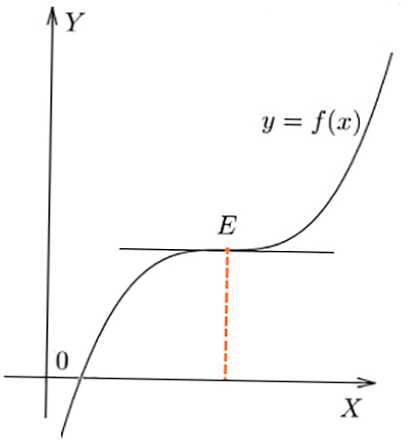
Pregib v točki E grafikona funkcije
Za raziskave f (x) sestavi shemo, kjer je vsak korak zgrajen v skladu z določenim algoritmom za izračun in analizo razmerij sestavnih elementov.
Razlike v funkciji in izpeljavi
Pravila seštevanja in odštevanja f (x) so enaka pravilom teh dejanj med diferenciacijo. Toda pravila za iskanje f '(x) pod dejanji množenja in delitve funkcij so različna (kot v tabeli).
Funkcija je primarna, izpeljanka pa sekundarna matematična operacija; v večini primerov imajo različne značilnosti.
Točka neprekinjene odvisnosti se nahaja po njenem drugem izvodu, njen znak pa naj se spremeni v območju točke x0.
Obstajajo takšne vrste funkcij, ki nimajo f '(x) v točki x0 (prekinitev). V izražanju ln (| x | -1) derivat ni določen v točki x0 = 1.
Obstajajo izrazi "modulo" podobno kot y = | x |, ki ima zgib v x0.
Za take odvisnosti se uporabljajo le delno (v intervalih definicijske domene) metode preučevanja njihovih lastnosti z uporabo izpeljank in ni vedno mogoče preklopiti z lastnosti f '(x) na lastnosti primarne.
Nikjer ne gre brez izjem med pravili in tudi pri matematiki. Za razčlenitev in utrjevanje predstavljenega gradiva je nujno treba rešiti primere, vaditi, pridobiti izkušnje z omejitvami, diferenciali in izpeljankami ter pogumno preiti na integrale.











